Confidence Intervals for Population Means

A confidence interval estimate consists of some interval of numbers, together with a measure of the likelihood that the interval contains the unknown population parameter we wish to estimate.

For example, if we say that a certain interval is 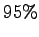$95\%$ confidence interval for the mean of a population, we mean the following:

If we were to repeat the process of constructing the confidence interval many times, each time with a new sample, then we expect the resulting interval to contain the population mean about 95% of the time, or 19 times out of 20.

In general, the confidence interval is determined by three things:

• The sample mean or point estimate $\overline{x}$
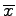
• Our level of confidence that the interval will contain the population mean $(1-\alpha)$
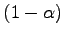
• The standard deviation of the sample mean

The subsections that follow cover three situations that we have considered.
They differ mainly in the way that the standard deviation of the sample mean is calculated:

• We want a confidence interval for the mean 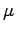$\mu$ of a population with (known) standard deviation $\sigma$
• We want a confidence interval for the mean 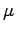$\mu$ of a population and must estimate the population standard deviation from the sample
• We want a confidence interval for the proportion of a population that has some characteristic