Obtaining t_alpha for a Left-tailed Region

If you know $\alpha$ and $n$ and want the value of $t_{\alpha}$ for a left-tailed region with probability $\alpha$ from a $t$ -distribution with $n$ degrees of freedom, the appropriate formula is:

   =TINV$$(2*\alpha,n)$$

You need to double the value of $\alpha$ because the function only returns two-sided values, that is, $t_{\alpha/2}$ . If you want $t_\alpha$ , you have to supply $2\cdot\alpha$ as the parameter.

For example, if $\alpha=0.05$ and the sample size (degrees of freedom) is $10$ , the formula is

   =TINV$$(2*0.05,10)$$

When this command executes, the result is $1.81$ , which is the value of $t_{\alpha}$ when we have $\alpha=0.05$ and $10$ degrees of freedom.

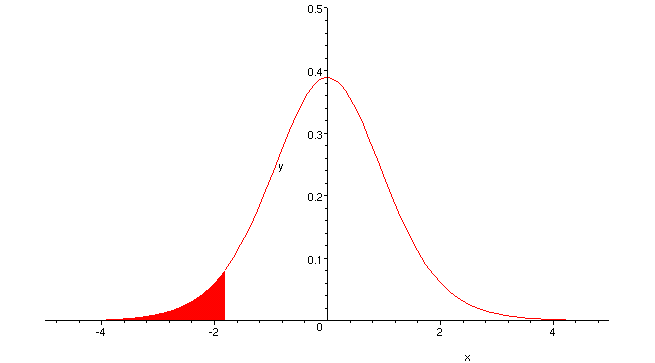
The graph below represents this result. The shaded area goes from $-\infty$ to $-1.81$ , and has total area equal to $\alpha$ , or $0.05$ .

Note that we changed the sign of the value that TINV returned. This is another consequence of the fact that TINV only returns two-tailed values, and we work around this limitation by using the fact that bell-shaped curves are symmetric, so the area under the curve from $1.81$ to $+\infty$ is the same as the area under the curve from $-\infty$ to $-1.81$ ; both areas are equal to $0.05$ which is our $\alpha$ value.

This threshold value would be used to construct a Left-tailed test or confidence region.

(Note: this is the correct syntax for Excel. It is slightly different for other spreadsheets. Consult the help menu of the spreadsheet you are using to find the correct syntax for your spreadsheet program).