Computational Details

Under the null hypothesis, the population has mean $\mu_0$ .

Using either the fact that the data are normal or the fact that the central limit theorem applies, assume that the data are from a normal distribution with mean $\mu_0$ .

With this assumption, if the null hypothesis is true, the sample mean $\overline{x}$ will also be normally distributed with mean $\mu_0$ .

If we use the sample standard deviation $s$ to calculate a test statistic $t$ as

$$t\;=\;\frac{\overline{x}-\mu_0}{s/\sqrt{n}}$$

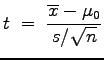
that statistic will have a $t$ -distribution with $n$ degrees of freedom.

The strategy for testing the hypothesis is to consider the sample mean as a single observation from the $t$ -distribution, which is bell-shaped, and base our decision to accept or reject the null hypothesis on where the $t$ -value falls on the bell-shaped curve of the $t$ -distribution.

We calculate the $t$ -stastic as:

$$t\;=\;\frac{\overline{x}-\mu_0}{s/\sqrt{n}}$$

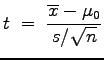
(This value is in cell B10)

The exact decision rule to accept or reject the null hypothesis depends on whether we want:

• a two-tailed test $(\mu\neq\mu_0)$
• a left-tailed $(\mu < \mu_0)$
• a right-tailed test. $(\mu > \mu_0)$

See the sections below for details on these three cases.